Funkcje wielomianowe i wymierne

  1. Narysuj wykres wielomianu:
    F(x) = (x – 1)(x – 2)(x – 3)
    F(x) = (x – 1)2(x – 2)
    F(x) = –(x – 1)(x – 2)(x + 3)
    F(x) = (x – 1)(x + 2)(x – 3)2.
  2. Rozwiąż równania wielomianowe:
    x3 + 2x2 –x – 2 = 0
    x3 + 4x2 –x – 4 = 0
    x3 + 3x2 –4x – 12 = 0.
  3. Rozwiąż nierówność wielomianową  x3 – 4x > 0.
  4. Dany jest wielomian W(x) = x3 – 5x2 – 9x + 45 sprawdź czy punkt A=(1,30) należy do wykresu  tego  wielomianu, oraz zapisz ten wielomian w postaci iloczynowej; narysuj wykres.
  5. Wielomian W(x) = ax4 + 5x3 + 9x2 – 15x – 9 jest podzielny przez dwumian (2x + 1). Wyznacz pierwiastki tego wielomianu.
  6. Wielomian W(x) = ax3 + bx2 + cx + d ma 3 miejsca zerowe x1 = – 2;  x2 = 1 i x3 = 2.
    Widząc ponadto, że W(–1) = 3 oblicz a.
  7. Liczby 3 i –1 są pierwiastkami wielomianu W(x) = 2x3 + ax2 + bx + 30. Wyznacz
    wartość współczynników a i b oraz oblicz trzeci pierwiastek.
  8. Dany jest wielomian W(x) = 2x3 + ax2 – 14x + b. Dla a = 0 i b = 0 otrzymujemy W(x) = 2x3 – 14x. Rozwiąż równanie 2×3 – 14x = 0 oraz dobierz tak wartości a i b w wielomianie W(x) = 2×3 + ax2 + bx + 30 by był on jednocześnie podzielny przez x – 2 i x + 3.
  9. Wykonaj dodawanie:
    \frac {x + 1} {x - 3} + \frac {x - 1} {x}
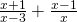
  10. Skróć ułamek:
    \frac {x - 2} {3x - 6}
  11. Rozwiąż równanie:
    \frac {4} {x + 3} = 1
    \frac {6} {x} = x + 5
    \frac {2x + 4} {2x - 1} = x - 1
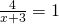
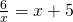
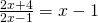
  12. Rozwiąż nierówność:
    \frac {3} {x}<-1 \frac {x + 1} {x + 2} > 1
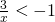
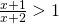
  13. Naszkicuj wykres funkcji y = \frac {x - 2} {x - 3}